Ridge and Lasso Regression
In this article, you will learn about two powerful regularization techniques in linear regression.
In this article, you will learn about two powerful regularization techniques in linear regression.
Laying the foundations
Before reading this article, you need to understand the basics of linear regression and the concept of overfitting.
To refresh your memory, this is what a linear regression model looks like:
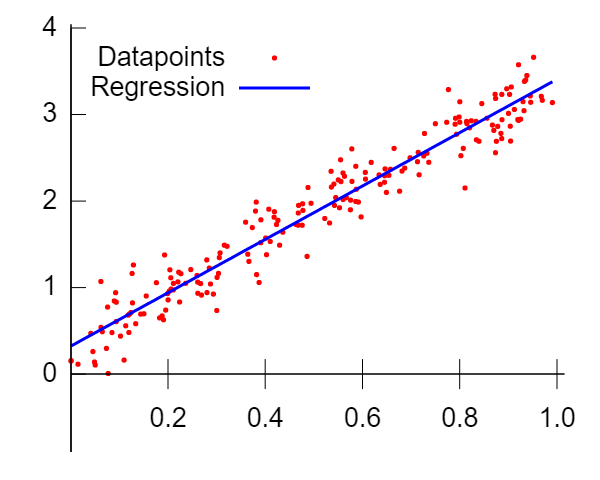
We fit a linear function onto all data points, and we use the independent variables X to predict the dependent variable Y.
If you aren't already familiar with how a linear regression model works, then please make sure to read this article.
In some cases, when we fit a linear regression model onto our data, we might encounter the issue of overfitting.
Overfitting is a phenomenon that takes place when a model fits very well onto a training dataset, but is unable to generalize to data that its never seen before.
If your model has very high training accuracy but low test accuracy, it means your model is overfitting.
Here's a diagram of what overfitting looks like (the blue line):
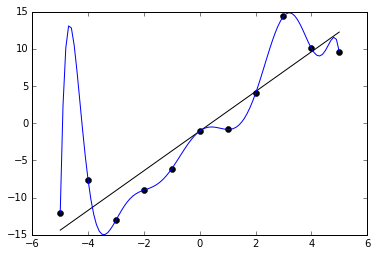
If you aren't already familiar with the concept, read my article on overfitting before coming to this one.
Mitigating overfitting
When you run a linear regression model in R or Python, a model will be created that fits best on all your data points.
This model will choose coefficients that minimizes the overall difference between true and predicted values.
Intuitively, as a model that chooses larger coefficients will increase in complexity.
So,
Larger coefficients = complex model
Smaller coefficients = simple model
This means that as the model chooses larger coefficients, it becomes more complex, which means it might overfit.
To mitigate overfitting, we need to force the model to choose smaller coefficients.
We can do this by employing a technique called regularization.
Regularization is a process that discourages the model from becoming overly complex.
It does this by punishing models that choose large coefficients.
Ridge regression
Now, you already know that our aim is to reduce model complexity.
We don't want our model to choose extremely large coefficients because that can lead to overfitting.
Ridge regression helps us achieve this by adding a penalty to the model's cost function.
It uses a technique called L2 regularization.
The cost function of a linear regression model is as follows:
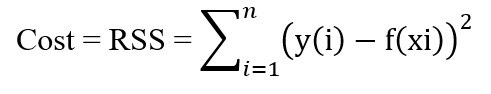
Our aim is to minimize the value shown above (the model's RSS), because we want the difference between our true and predicted value to be as small as possible.
In ridge regression, we include an additional parameter to the cost function so it becomes:
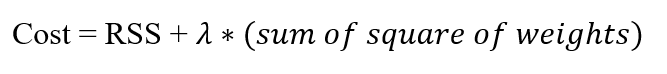
We add the sum of square of model weights to the cost function.
This means that the model's cost increases as it chooses larger weights (larger coefficients).
This additional parameter acts as a constraint, and the model is now forced to choose smaller coefficients.
You must have noticed that we multiply the sum of square of weights with the Greek symbol lambda.
In the equation above,
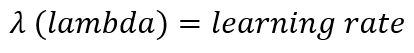
This is a very small value (usually ranging from 0 to 0.1), and determines the magnitude of penalty that will be imposed onto the model.
For example:
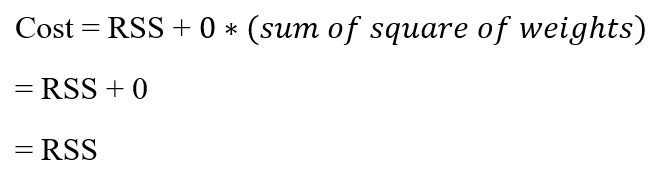
If we choose lambda as 0, then the cost is just the RSS. Even large weights won't have an impact on the model.
So the closer the weight decay is to 0, the lesser our model gets punished for choosing large coefficients.
For example:
- Lets find the cost of a model with a small value of lambda:
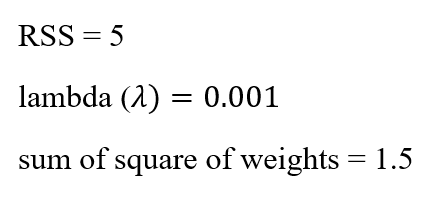
When plugging these values into the formula above, the cost becomes 5.0015.
2. Now, if we increase the value of lambda to 0.01, the cost becomes 5.015.
The cost becomes a lot higher as we increase the value of lambda. We can change the values of lambda depending on our aim.
If we want a model that generalizes better and heavily penalizes large coefficients, then we can choose a larger value of lambda.
Lasso regression
Lasso regression uses a technique called L1 regularization.
It does the same thing as ridge regression does - it adds a penalty to the cost function so that larger weights get penalized.
The only difference is in the formula - instead of adding the sum of square of weights, lasso regression adds the absolute value of weights to the cost.
The formula for lasso regression is as follows:
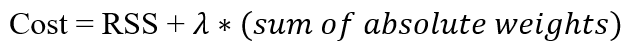
It works similar to ridge regression it terms of mitigating overfitting, except that it takes the absolute weights instead of the square weights.
Feature selection
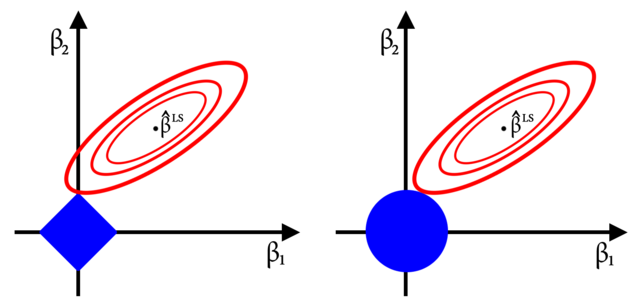
If you want to perform linear regression on a high dimensional dataset, lasso regression can help you narrow down and eliminate some features.
Both ridge and lasso regression will help shrink coefficients, and minimize feature weights.
However, if the value of lambda is large enough, lasso regression can sometimes pull feature weights down to zero.
When the coefficient of a feature gets pulled down to zero, that coefficient is eliminated from the model.
This way, lasso regression can help eliminate unnecessary features from your model.
It should be noted that ridge regression does not set coefficients to zero, so it can't be used to eliminate features the way lasso regression can.